Skip to contents

UniFrac Calculations

Source: vignettes/unifrac.Rmd
unifrac.Rmd

Introduction

The different UniFrac algorithms are listed below, along with examples for calculating them.


Input Data

  • A numeric matrix with two samples and five species.
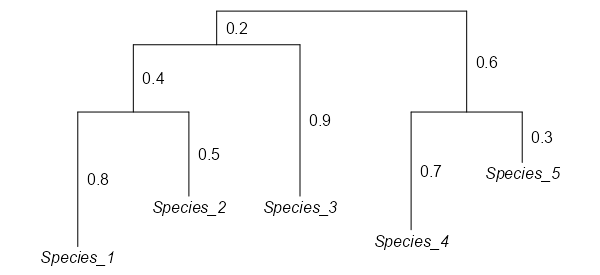
  • A phylogenetic tree for those five species.
Sample_A Sample_B
Species_1 0 1
Species_2 0 4
Species_3 9 2
Species_4 3 8
Species_5 3 0


Definitions

The branch indices (green circles) are used for ordering the L, A, and B arrays. Values for L are drawn from the input phylogenetic tree. Values for A and B are the total number of species observations descending from that branch; A for Sample_A, and B for Sample_B.


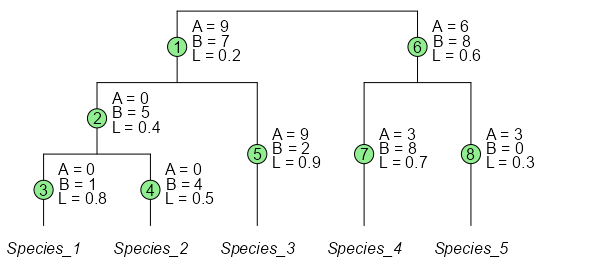
n = 8 Number of branches
A = \{9, 0, 0, 0, 9, 6, 3, 3\} Branch weights for Sample_A.
B = \{7, 5, 1, 4, 2, 8, 8, 0\} Branch weights for Sample_B.
A_T = 15 Total observations for Sample_A.
B_T = 15 Total observations for Sample_B.
L = \{0.2, 0.4, 0.8, 0.5, 0.9, 0.6, 0.7, 0.3\} The branch lengths.


Unweighted

First, transform A and B into presence (1) and absence (0) indicators.

\begin{align*} A &= \{9, 0, 0, 0, 9, 6, 3, 3\} \\ A' &= \{1, 0, 0, 0, 1, 1, 1, 1\} \end{align*}

\begin{align*} B &= \{7, 5, 1, 4, 2, 8, 8, 0\} \\ B' &= \{1, 1, 1, 1, 1, 1, 1, 0\} \end{align*}

Then apply the formula:

\begin{align*} U &= \displaystyle \frac{\sum_{i = 1}^{n} L_i(|A'_i - B'_i|)}{\sum_{i = 1}^{n} L_i(max(A'_i,B'_i))} \\ \\ U &= \displaystyle \frac{L_1(|A'_1-B'_1|) + L_2(|A'_2-B'_2|) + \cdots + L_n(|A'_n-B'_n|)}{L_1(max(A'_1,B'_1)) + L_2(max(A'_2,B'_2)) + \cdots + L_n(max(A'_n,B'_n))} \\ \\ U &= \displaystyle \frac{0.2(|1-1|) + 0.4(|0-1|) + \cdots + 0.3(|1-0|)}{0.2(max(1,1)) + 0.4(max(0,1)) + \cdots + 0.3(max(1,0))} \\ \\ U &= \displaystyle \frac{0.2(0) + 0.4(1) + 0.8(1) + 0.5(1) + 0.9(0) + 0.6(0) + 0.7(0) + 0.3(1)}{0.2(1) + 0.4(1) + 0.8(1) + 0.5(1) + 0.9(1) + 0.6(1) + 0.7(1) + 0.3(1)} \\ \\ U &= \displaystyle \frac{0.4 + 0.8 + 0.5 + 0.3}{0.2 + 0.4 + 0.8 + 0.5 + 0.9 + 0.6 + 0.7 + 0.3} \\ \\ U &= \displaystyle \frac{2}{4.4} \\ \\ U &= 0.4545455 \end{align*}

Weighted

\begin{align*} W &= \sum_{i = 1}^{n} L_i|\frac{A_i}{A_T} - \frac{B_i}{B_T}| \\ \\ W &= L_1|\frac{A_1}{A_T} - \frac{B_1}{B_T}| + L_2|\frac{A_2}{A_T} - \frac{B_2}{B_T}| + \cdots + L_n|\frac{A_n}{A_T} - \frac{B_n}{B_T}| \\ \\ W &= 0.2|\frac{9}{15} - \frac{7}{15}| + 0.4|\frac{0}{15} - \frac{5}{15}| + \cdots + 0.3|\frac{3}{15} - \frac{0}{15}| \\ \\ W &= 0.02\overline{6} + 0.1\overline{3} + 0.05\overline{3} + 0.1\overline{3} + 0.42 + 0.08 + 0.2\overline{3} + 0.06 \\ \\ W &= 1.14 \end{align*}

Normalized

\begin{align*} N &= \displaystyle \frac {\sum_{i = 1}^{n} L_i|\frac{A_i}{A_T} - \frac{B_i}{B_T}|} {\sum_{i = 1}^{n} L_i(\frac{A_i}{A_T} + \frac{B_i}{B_T})} \\ \\ N &= \displaystyle \frac {L_1|\frac{A_1}{A_T} - \frac{B_1}{B_T}| + L_2|\frac{A_2}{A_T} - \frac{B_2}{B_T}| + \cdots + L_n|\frac{A_n}{A_T} - \frac{B_n}{B_T}|} {L_1(\frac{A_1}{A_T} + \frac{B_1}{B_T}) + L_2(\frac{A_2}{A_T} + \frac{B_2}{B_T}) + \cdots + L_n(\frac{A_n}{A_T} + \frac{B_n}{B_T})} \\ \\ N &= \displaystyle \frac {0.2|\frac{9}{15} - \frac{7}{15}| + 0.4|\frac{0}{15} - \frac{5}{15}| + \cdots + 0.3|\frac{3}{15} - \frac{0}{15}|} {0.2(\frac{9}{15} + \frac{7}{15}) + 0.4(\frac{0}{15} + \frac{5}{15}) + \cdots + 0.3(\frac{3}{15} + \frac{0}{15})} \\ \\ N &= \displaystyle \frac {0.02\overline{6} + 0.1\overline{3} + 0.05\overline{3} + 0.1\overline{3} + 0.42 + 0.08 + 0.2\overline{3} + 0.06} {0.21\overline{3} + 0.1\overline{3} + 0.05\overline{3} + 0.1\overline{3} + 0.66 + 0.56 + 0.51\overline{3} + 0.06} \\ \\ N &= \displaystyle \frac{1.14}{2.326667} \\ \\ N &= 0.4899713 \end{align*}

Generalized

  • Chen et al. 2012: Generalized UniFrac
  • R Package ecodive: generalized_unifrac(alpha = 0.5)
  • R Package abdiv: generalized_unifrac(alpha = 0.5)
  • R Package GUniFrac: GUniFrac(alpha = 0.5)
  • qiime2 qiime diversity beta-phylogenetic --p-metric generalized_unifrac -a 0.5

\begin{align*} G &= \displaystyle \frac {\sum_{i = 1}^{n} L_i(\frac{A_i}{A_T} + \frac{B_i}{B_T})^{\alpha} |\displaystyle \frac {\frac{A_i}{A_T} - \frac{B_i}{B_T}} {\frac{A_i}{A_T} + \frac{B_i}{B_T}} |} {\sum_{i = 1}^{n} L_i(\frac{A_i}{A_T} + \frac{B_i}{B_T})^{\alpha}} \\ \\ G &= \displaystyle \frac { L_1(\frac{A_1}{A_T} + \frac{B_1}{B_T})^{0.5} |\displaystyle \frac {\frac{A_1}{A_T} - \frac{B_1}{B_T}} {\frac{A_1}{A_T} + \frac{B_1}{B_T}}| + \cdots + L_n(\frac{A_n}{A_T} + \frac{B_n}{B_T})^{0.5} |\displaystyle \frac {\frac{A_n}{A_T} - \frac{B_n}{B_T}} {\frac{A_n}{A_T} + \frac{B_n}{B_T}}| }{ L_1(\frac{A_1}{A_T} + \frac{B_1}{B_T})^{0.5} + \cdots + L_n(\frac{A_n}{A_T} + \frac{B_n}{B_T})^{0.5} } \\ \\ G &= \displaystyle \frac { 0.2(\frac{9}{15} + \frac{7}{15})^{0.5} |\displaystyle \frac {\frac{9}{15} - \frac{7}{15}} {\frac{9}{15} + \frac{7}{15}}| + \cdots + 0.3(\frac{3}{15} + \frac{0}{15})^{0.5} |\displaystyle \frac {\frac{3}{15} - \frac{0}{15}} {\frac{3}{15} + \frac{0}{15}}| }{ 0.2(\frac{9}{15} + \frac{7}{15})^{0.5} + \cdots + 0.3(\frac{3}{15} + \frac{0}{15})^{0.5} } \\ \\ G &\approx \displaystyle \frac {0.03 + 0.23 + 0.21 + 0.26 + 0.49 + 0.08 + 0.27 + 0.13} {0.21 + 0.23 + 0.21 + 0.26 + 0.77 + 0.58 + 0.60 + 0.13} \\ \\ G &= \displaystyle \frac{1.701419}{2.986235} \\ \\ G &= 0.569754 \end{align*}

Variance Adjusted

\begin{align*} V &= \displaystyle \frac {\sum_{i = 1}^{n} L_i\displaystyle \frac {|\frac{A_i}{A_T} - \frac{B_i}{B_T}|} {\sqrt{(A_i + B_i)(A_T + B_T - A_i - B_i)}} } {\sum_{i = 1}^{n} L_i\displaystyle \frac {\frac{A_i}{A_T} + \frac{B_i}{B_T}} {\sqrt{(A_i + B_i)(A_T + B_T - A_i - B_i)}} } \\ \\ V &= \displaystyle \frac { L_1\displaystyle \frac {|\frac{A_1}{A_T} - \frac{B_1}{B_T}|} {\sqrt{(A_1 + B_1)(A_T + B_T - A_1 - B_1)}} + \cdots + L_n\displaystyle \frac {|\frac{A_n}{A_T} - \frac{B_n}{B_T}|} {\sqrt{(A_n + B_n)(A_T + B_T - A_n - B_n)}} }{ L_1\displaystyle \frac {\frac{A_1}{A_T} + \frac{B_1}{B_T}} {\sqrt{(A_1 + B_1)(A_T + B_T - A_1 - B_1)}} + \cdots + L_n\displaystyle \frac {\frac{A_n}{A_T} + \frac{B_n}{B_T}} {\sqrt{(A_n + B_n)(A_T + B_T - A_n - B_n)}} } \\ \\ V &= \displaystyle \frac { 0.2\displaystyle \frac {|\frac{9}{15} - \frac{7}{15}|} {\sqrt{(9 + 7)(15 + 15 - 9 - 7)}} + \cdots + 0.3\displaystyle \frac {|\frac{3}{15} - \frac{0}{15}|} {\sqrt{(3 + 0)(15 + 15 - 3 - 0)}} }{ 0.2\displaystyle \frac {\frac{9}{15} + \frac{7}{15}} {\sqrt{(9 + 7)(15 + 15 - 9 - 7)}} + \cdots + 0.3\displaystyle \frac {\frac{3}{15} + \frac{0}{15}} {\sqrt{(3 + 0)(15 + 15 - 3 - 0)}} } \\ \\ V &\approx \displaystyle \frac {0.002 + 0.012 + 0.010 + 0.013 + 0.029 + 0.005 + 0.016 + 0.007} {0.014 + 0.012 + 0.010 + 0.013 + 0.046 + 0.037 + 0.036 + 0.007} \\ \\ V &= \displaystyle \frac{4.09389}{4.174402} \\ \\ V &= 0.9807128 \end{align*}