Skip to contents

UniFrac Algorithms

Source: vignettes/articles/unifrac.Rmd
unifrac.Rmd

Introduction

The different UniFrac algorithms are listed below, along with examples for calculating them.


Input Data 


json <- '{"id":"","comment":"","date":"2025-01-29T22:14:00Z","format":"1.0.0","type":"OTU table","format_url":"http://biom-format.org","generated_by":"rbiom 2.0.13","matrix_type":"sparse","matrix_element_type":"int","shape":[5,2],"phylogeny":"(((OTU_1:0.8,OTU_2:0.5):0.4,OTU_3:0.9):0.2,(OTU_4:0.7,OTU_5:0.3):0.6);","rows":{"1":{"id":"OTU_1"},"2":{"id":"OTU_2"},"3":{"id":"OTU_3"},"4":{"id":"OTU_4"},"5":{"id":"OTU_5"}},"columns":[{"id":"Sample_1"},{"id":"Sample_2"}],"data":[[2,0,9],[3,0,3],[4,0,3],[0,1,1],[1,1,4],[2,1,2],[3,1,8]]}'

biom <- rbiom::as_rbiom(json, underscores = TRUE)
mtx  <- t(as.matrix(biom))
phy  <- biom$tree

L <- phy$edge.length
A <- c(9,0,0,0,9,6,3,3)
B <- c(7,5,1,4,2,8,8,0)
  • An OTU matrix with two samples and five OTUs.
  • A phylogenetic tree for those five OTUs.
knitr::kable(mtx, format="html", table.attr='class="otu_matrix" cellspacing="0"', align='c')
OTU_1 OTU_2 OTU_3 OTU_4 OTU_5
Sample_1 0 0 9 3 3
Sample_2 1 4 2 8 0 


par(xpd = NA)
plot(
  x          = phy, 
  direction  = 'downwards', 
  srt        = 90, 
  adj        = 0.5, 
  no.margin  = TRUE,
  underscore = TRUE,
  x.lim      = c(0.5, 5.5) )

ape::edgelabels(phy$edge.length, bg = 'white', frame = 'none', adj = -0.4)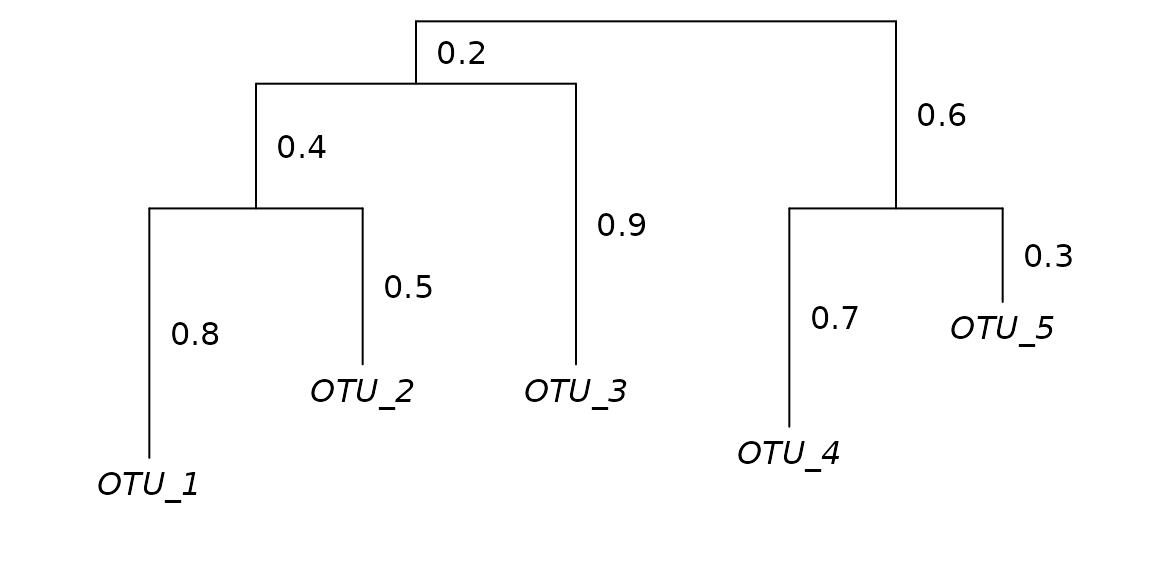


Definitions

The branch indices (green circles) are used for ordering the LL, AA, and BB arrays. Values for LL are drawn from the input phylogenetic tree. Values for AA and BB are the total number of OTU observations descending from that branch; AA for Sample_1, and BB for Sample_2.

local({
  
  phy$edge.length <- c(1, 1, 1, 1, 2, 1, 2, 2)
  
  par(xpd = NA)
  plot(
    x               = phy, 
    direction       = 'downwards', 
    srt             = 90, 
    adj             = 0.5, 
    no.margin       = TRUE,
    underscore      = TRUE,
    x.lim           = c(.8, 6) )
  
  ape::edgelabels(1:8, frame = 'circle')
  
  ape::edgelabels(paste('A =', A), bg = 'white', frame = 'none', adj = c(-0.4, -1.2))
  ape::edgelabels(paste('B =', B), bg = 'white', frame = 'none', adj = c(-0.4,  0.0))
  ape::edgelabels(paste('L =', L), bg = 'white', frame = 'none', adj = c(-0.3,  1.2))
})


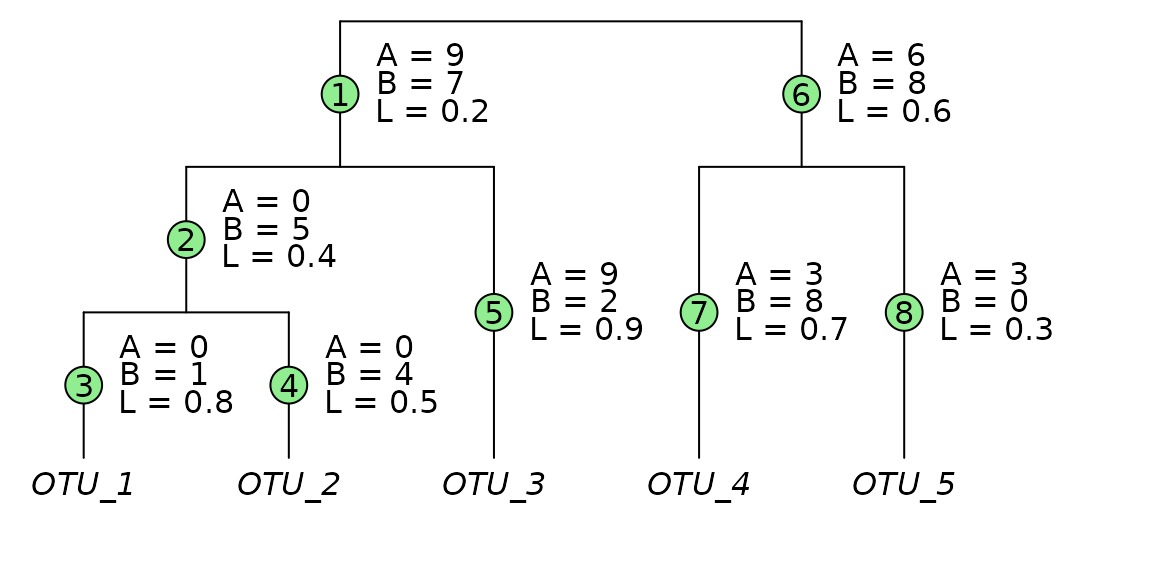
n=8n = 8 Number of branches
A={9,0,0,0,9,6,3,3}A = \{9, 0, 0, 0, 9, 6, 3, 3\} Branch weights for Sample_1.
B={7,5,1,4,2,8,8,0}B = \{7, 5, 1, 4, 2, 8, 8, 0\} Branch weights for Sample_2.
AT=15A_T = 15 Total OTU counts for Sample_1.
BT=15B_T = 15 Total OTU counts for Sample_2.
L={0.2,0.4,0.8,0.5,0.9,0.6,0.7,0.3}L = \{0.2, 0.4, 0.8, 0.5, 0.9, 0.6, 0.7, 0.3\} The branch lengths.


Unweighted

  • Lozupone et al, 2005: Unweighted UniFrac
  • R Package rbiom: bdiv_matrix(bdiv = "unifrac", weighted=FALSE)
  • R Package phyloseq: UniFrac(weighted=FALSE)
  • R Package abdiv: unweighted_unifrac()
  • qiime2 qiime diversity beta-phylogenetic --p-metric unweighted_unifrac
  • mothur: unifrac.unweighted()

First, transform A and B into presence (1) and absence (0) indicators.

A={9,0,0,0,9,6,3,3}A′={1,0,0,0,1,1,1,1}\begin{align*} A &= \{9, 0, 0, 0, 9, 6, 3, 3\} \\ A' &= \{1, 0, 0, 0, 1, 1, 1, 1\} \end{align*}

B={7,5,1,4,2,8,8,0}B′={1,1,1,1,1,1,1,0}\begin{align*} B &= \{7, 5, 1, 4, 2, 8, 8, 0\} \\ B' &= \{1, 1, 1, 1, 1, 1, 1, 0\} \end{align*}

Then apply the formula:

U=∑i=1nLi(|A′i−B′i|)∑i=1nLi(max(A′i,B′i))U=L1(|A′1−B′1|)+L2(|A′2−B′2|)+⋯+Ln(|A′n−B′n|)L1(max(A′1,B′1))+L2(max(A′2,B′2))+⋯+Ln(max(A′n,B′n))U=0.2(|1−1|)+0.4(|0−1|)+⋯+0.3(|1−0|)0.2(max(1,1))+0.4(max(0,1))+⋯+0.3(max(1,0))U=0.2(0)+0.4(1)+0.8(1)+0.5(1)+0.9(0)+0.6(0)+0.7(0)+0.3(1)0.2(1)+0.4(1)+0.8(1)+0.5(1)+0.9(1)+0.6(1)+0.7(1)+0.3(1)U=0.4+0.8+0.5+0.30.2+0.4+0.8+0.5+0.9+0.6+0.7+0.3U=24.4U=0.4545455\begin{align*} U &= \displaystyle \frac{\sum_{i = 1}^{n} L_i(|A'_i - B'_i|)}{\sum_{i = 1}^{n} L_i(max(A'_i,B'_i))} \\ \\ U &= \displaystyle \frac{L_1(|A'_1-B'_1|) + L_2(|A'_2-B'_2|) + \cdots + L_n(|A'_n-B'_n|)}{L_1(max(A'_1,B'_1)) + L_2(max(A'_2,B'_2)) + \cdots + L_n(max(A'_n,B'_n))} \\ \\ U &= \displaystyle \frac{0.2(|1-1|) + 0.4(|0-1|) + \cdots + 0.3(|1-0|)}{0.2(max(1,1)) + 0.4(max(0,1)) + \cdots + 0.3(max(1,0))} \\ \\ U &= \displaystyle \frac{0.2(0) + 0.4(1) + 0.8(1) + 0.5(1) + 0.9(0) + 0.6(0) + 0.7(0) + 0.3(1)}{0.2(1) + 0.4(1) + 0.8(1) + 0.5(1) + 0.9(1) + 0.6(1) + 0.7(1) + 0.3(1)} \\ \\ U &= \displaystyle \frac{0.4 + 0.8 + 0.5 + 0.3}{0.2 + 0.4 + 0.8 + 0.5 + 0.9 + 0.6 + 0.7 + 0.3} \\ \\ U &= \displaystyle \frac{2}{4.4} \\ \\ U &= 0.4545455 \end{align*}

Weighted

  • Lozupone et al, 2007: Raw Weighted UniFrac
  • R Package rbiom: bdiv_matrix(bdiv = "unifrac", weighted=TRUE, normalized=FALSE)
  • R Package phyloseq: UniFrac(weighted=TRUE, normalized=FALSE)
  • R Package abdiv: weighted_unifrac()
  • qiime2 qiime diversity beta-phylogenetic --p-metric weighted_unifrac

W=∑i=1nLi|AiAT−BiBT|W=L1|A1AT−B1BT|+L2|A2AT−B2BT|+⋯+Ln|AnAT−BnBT|W=0.2|915−715|+0.4|015−515|+⋯+0.3|315−015|W=0.026¯+0.13¯+0.053¯+0.13¯+0.42+0.08+0.23¯+0.06W=1.14\begin{align*} W &= \sum_{i = 1}^{n} L_i|\frac{A_i}{A_T} - \frac{B_i}{B_T}| \\ \\ W &= L_1|\frac{A_1}{A_T} - \frac{B_1}{B_T}| + L_2|\frac{A_2}{A_T} - \frac{B_2}{B_T}| + \cdots + L_n|\frac{A_n}{A_T} - \frac{B_n}{B_T}| \\ \\ W &= 0.2|\frac{9}{15} - \frac{7}{15}| + 0.4|\frac{0}{15} - \frac{5}{15}| + \cdots + 0.3|\frac{3}{15} - \frac{0}{15}| \\ \\ W &= 0.02\overline{6} + 0.1\overline{3} + 0.05\overline{3} + 0.1\overline{3} + 0.42 + 0.08 + 0.2\overline{3} + 0.06 \\ \\ W &= 1.14 \end{align*}

Normalized

  • Lozupone et al, 2007: Normalized Weighted UniFrac
  • R Package rbiom: bdiv_matrix(bdiv = "unifrac", weighted=TRUE, normalized=TRUE)
  • R Package phyloseq: UniFrac(weighted=TRUE, normalized=TRUE)
  • R Package abdiv: weighted_normalized_unifrac()
  • qiime2 qiime diversity beta-phylogenetic --p-metric weighted_normalized_unifrac
  • mothur: unifrac.weighted()

N=∑i=1nLi|AiAT−BiBT|∑i=1nLi(AiAT+BiBT)N=L1|A1AT−B1BT|+L2|A2AT−B2BT|+⋯+Ln|AnAT−BnBT|L1(A1AT+B1BT)+L2(A2AT+B2BT)+⋯+Ln(AnAT+BnBT)N=0.2|915−715|+0.4|015−515|+⋯+0.3|315−015|0.2(915+715)+0.4(015+515)+⋯+0.3(315+015)N=0.026¯+0.13¯+0.053¯+0.13¯+0.42+0.08+0.23¯+0.060.213¯+0.13¯+0.053¯+0.13¯+0.66+0.56+0.513¯+0.06N=1.142.326667N=0.4899713\begin{align*} N &= \displaystyle \frac {\sum_{i = 1}^{n} L_i|\frac{A_i}{A_T} - \frac{B_i}{B_T}|} {\sum_{i = 1}^{n} L_i(\frac{A_i}{A_T} + \frac{B_i}{B_T})} \\ \\ N &= \displaystyle \frac {L_1|\frac{A_1}{A_T} - \frac{B_1}{B_T}| + L_2|\frac{A_2}{A_T} - \frac{B_2}{B_T}| + \cdots + L_n|\frac{A_n}{A_T} - \frac{B_n}{B_T}|} {L_1(\frac{A_1}{A_T} + \frac{B_1}{B_T}) + L_2(\frac{A_2}{A_T} + \frac{B_2}{B_T}) + \cdots + L_n(\frac{A_n}{A_T} + \frac{B_n}{B_T})} \\ \\ N &= \displaystyle \frac {0.2|\frac{9}{15} - \frac{7}{15}| + 0.4|\frac{0}{15} - \frac{5}{15}| + \cdots + 0.3|\frac{3}{15} - \frac{0}{15}|} {0.2(\frac{9}{15} + \frac{7}{15}) + 0.4(\frac{0}{15} + \frac{5}{15}) + \cdots + 0.3(\frac{3}{15} + \frac{0}{15})} \\ \\ N &= \displaystyle \frac {0.02\overline{6} + 0.1\overline{3} + 0.05\overline{3} + 0.1\overline{3} + 0.42 + 0.08 + 0.2\overline{3} + 0.06} {0.21\overline{3} + 0.1\overline{3} + 0.05\overline{3} + 0.1\overline{3} + 0.66 + 0.56 + 0.51\overline{3} + 0.06} \\ \\ N &= \displaystyle \frac{1.14}{2.326667} \\ \\ N &= 0.4899713 \end{align*}

Generalized

  • Chen et al. 2012: Generalized UniFrac
  • R Package GUniFrac: GUniFrac(alpha=0.5)
  • R Package abdiv: generalized_unifrac(alpha = 0.5)
  • qiime2 qiime diversity beta-phylogenetic --p-metric generalized_unifrac -a 0.5

G=∑i=1nLi(AiAT+BiBT)0.5|AiAT−BiBTAiAT+BiBT|∑i=1nLi(AiAT+BiBT)0.5G=L1(A1AT+B1BT)0.5|A1AT−B1BTA1AT+B1BT|+⋯+Ln(AnAT+BnBT)0.5|AnAT−BnBTAnAT+BnBT|L1(A1AT+B1BT)0.5+⋯+Ln(AnAT+BnBT)0.5G=0.2(915+715)0.5|915−715915+715|+⋯+0.3(315+015)0.5|315−015315+015|0.2(915+715)0.5+⋯+0.3(315+015)0.5G≈0.03+0.23+0.21+0.26+0.49+0.08+0.27+0.130.21+0.23+0.21+0.26+0.77+0.58+0.60+0.13G=1.7014192.986235G=0.569754\begin{align*} G &= \displaystyle \frac {\sum_{i = 1}^{n} L_i(\frac{A_i}{A_T} + \frac{B_i}{B_T})^{0.5} |\displaystyle \frac {\frac{A_i}{A_T} - \frac{B_i}{B_T}} {\frac{A_i}{A_T} + \frac{B_i}{B_T}} |} {\sum_{i = 1}^{n} L_i(\frac{A_i}{A_T} + \frac{B_i}{B_T})^{0.5}} \\ \\ G &= \displaystyle \frac { L_1(\frac{A_1}{A_T} + \frac{B_1}{B_T})^{0.5} |\displaystyle \frac {\frac{A_1}{A_T} - \frac{B_1}{B_T}} {\frac{A_1}{A_T} + \frac{B_1}{B_T}}| + \cdots + L_n(\frac{A_n}{A_T} + \frac{B_n}{B_T})^{0.5} |\displaystyle \frac {\frac{A_n}{A_T} - \frac{B_n}{B_T}} {\frac{A_n}{A_T} + \frac{B_n}{B_T}}| }{ L_1(\frac{A_1}{A_T} + \frac{B_1}{B_T})^{0.5} + \cdots + L_n(\frac{A_n}{A_T} + \frac{B_n}{B_T})^{0.5} } \\ \\ G &= \displaystyle \frac { 0.2(\frac{9}{15} + \frac{7}{15})^{0.5} |\displaystyle \frac {\frac{9}{15} - \frac{7}{15}} {\frac{9}{15} + \frac{7}{15}}| + \cdots + 0.3(\frac{3}{15} + \frac{0}{15})^{0.5} |\displaystyle \frac {\frac{3}{15} - \frac{0}{15}} {\frac{3}{15} + \frac{0}{15}}| }{ 0.2(\frac{9}{15} + \frac{7}{15})^{0.5} + \cdots + 0.3(\frac{3}{15} + \frac{0}{15})^{0.5} } \\ \\ G &\approx \displaystyle \frac {0.03 + 0.23 + 0.21 + 0.26 + 0.49 + 0.08 + 0.27 + 0.13} {0.21 + 0.23 + 0.21 + 0.26 + 0.77 + 0.58 + 0.60+ 0.13} \\ \\ G &= \displaystyle \frac{1.701419}{2.986235} \\ \\ G &= 0.569754 \end{align*}

Variance Adjusted

  • Chang et al, 2011: Variance Adjusted Weighted (VAW) UniFrac
  • R Package abdiv: variance_adjusted_unifrac()
  • qiime2 qiime diversity beta-phylogenetic --p-metric weighted_normalized_unifrac --p-variance-adjusted

V=∑i=1nLi|AiAT−BiBT|(AT+BT)(AT+BT−Ai−Bi)∑i=1nLiAiAT+BiBT(AT+BT)(AT+BT−Ai−Bi)\begin{align*} V &= \displaystyle \frac {\sum_{i = 1}^{n} L_i\displaystyle \frac {|\frac{A_i}{A_T} - \frac{B_i}{B_T}|} {(A_T + B_T)(A_T + B_T - A_i - B_i)} } {\sum_{i = 1}^{n} L_i\displaystyle \frac {\frac{A_i}{A_T} + \frac{B_i}{B_T}} {(A_T + B_T)(A_T + B_T - A_i - B_i)} } \\ \\ \end{align*}